더보기
21일 차 회고.
토이 프로젝트에 경진대회에 자격증까지 해야 할 일이 많아서 너무 힘든 날이었다.
1. Supervised Learning - Regression
1-1. Regression 평가 지표
Linear Regression
from sklearn.datasets import load_diabetes
diabetes = load_diabetes()
data = diabetes.data
target = diabetes.target
from sklearn.model_selection import train_test_split
SEED = 42
x_train, x_valid , y_train, y_valid = train_test_split(data, target, random_state=SEED)
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(x_train,y_train)
pred = model.predict(x_valid)
R2(Coefficient of Determination; 결정계수)
- 회귀식이 얼마나 정확한지를 나타낸다.


- R2의 값은 0에서 1 사이의 값을 가진다.

from sklearn.metrics import r2_score
r2 = r2_score(y_valid, pred)
MSE(Mean Squared Error)
- 실제값과 예측값의 차이의 제곱의 평균을 나타낸다.
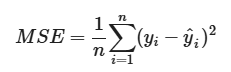
- MSE는 이상치에 민감하며, 직관적이지 못하다.
from sklearn.metrics import mean_squared_error
mse = mse_squared_error(y_valid, pred)
RMSE(Root Mean Squared Error)
- MSE의 제곱근을 나타낸다.

- RMSE 또한 이상치에 민감하다.
import numpy as np
np.sqrt(mse)
RMSLE(Root Mean Squared Logarithmic Error)
- 실제값과 예측값의 로그 차이의 제곱의 평균의 제곱근을 나타낸다.

- 값이 작을수록 오류가 적다.
df rmsle(y, pred, converetExp=False):
if convertExp:
y = np.exp(y)
pred = np.exp(pred)
log1 = np.nan_to_num(np.array([np.log(v + 1) for v in y]))
log2 = np.nan_to_num(np.array([np.log(v + 1) for v in pred]))
calc = (log1 - log2)**2
return np.sqrt(np.mean(calc))
rmsle_score = rmsle(y_valid, pred)
MAE(Mean Absolute Error)
- 실제값과 예측값의 차이의 절댓값의 평균을 나타낸다.

- 손실함수로 주로 사용한다.
from sklearn.metrics import mean_absolute_error
mae = mean_absolute_error(y_valid, pred)
MAPE(Mean Absolute Percentage Error)
- 실제값에 대한 절대오차 비율의 평균을 백분율로 표현한다.

- MAPE는 0에서 1 사이의 값을 가진다.
- 0에 가까울수록 학습이 잘 됐다는 것을 나타낸다.
from sklearn.metrics import mean_absolute_percentage_error
mape = mean_absolute_percentage_error(y_valid, pred)
SMAPE(Symmetric Mean Absolute Percentage Error)

- 실제값에 0이 존재해도 계산이 가능하다.
def smape(true, pred):
error = np.abs(true - pred) / (np.abs(true) + np.abs(pred))
return np.mean(error)
smape(y_valid, pred)
1-2. 경사하강법
Linear Regression
- 단순 선형 회귀식

- 가중치(w)와 절편(b)을 MSE를 최소화하는 방법으로 구할 수 있다.

손실함수


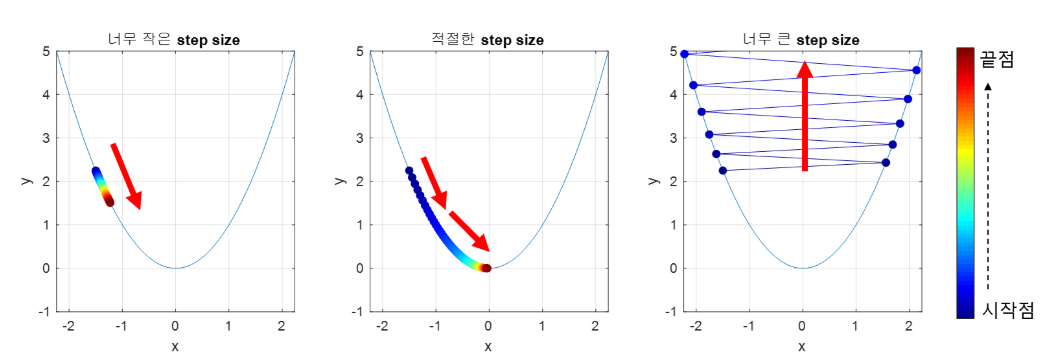
Learning Rate
- Learning Rate가 작을 경우, 학습이 오래 걸린다.
- Learning Rate가 클 경우, 학습이 되지 않을 수 있다.
코드 구현
import numpy as np
import matplotlib.pyplot as plt
X = np.random.rand(100)
Y = 0.3 * X + 1.5
plt.figure(figsize=(8, 6))
plt.scatter(X, Y)
plt.show()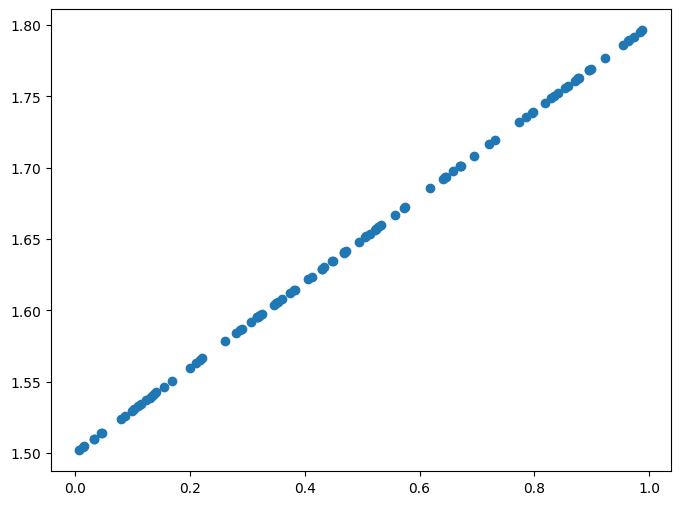
def plot_prediction(pred, y, W, b):
plt.figure(figsize=(8, 6))
plt.scatter(X, y)
plt.scatter(X, pred)
plt.title(f"W: {W} / b: {b}")
plt.show()
W = np.random.uniform(-1, 1)
b = np.random.uniform(-1, 1)
learning_rate = 0.7
for epoch in range(200):
Y_pred = W * X + b
error = np.abs(Y_pred - Y).mean()
if error < 0.001: # 학습 완료
break
w_grad = learning_rate * ((Y_pred - Y) * X).mean()
b_grad = learning_rate * ((Y_pred - Y) * 1).mean()
W = W - w_grad
b = b - b_grad
if epoch % 10 == 0:
Y_pred = W * X + b
plot_prediction(Y_pred, Y, W, b)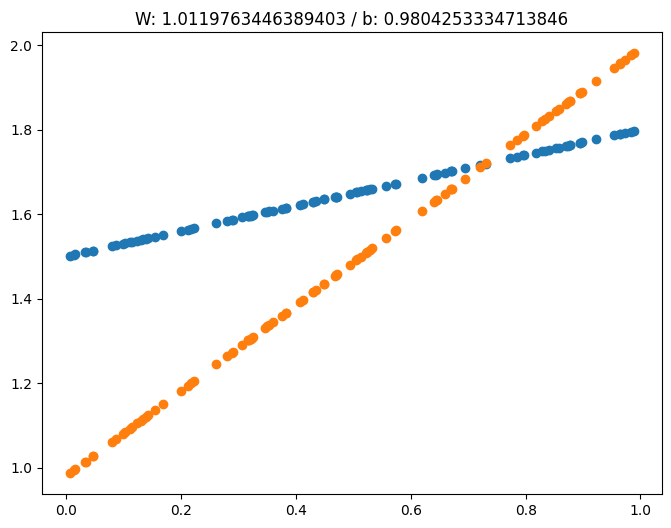

1-3. 모델
필수 라이브러리
!pip install --upgrade joblib==1.1.0
!pip install --upgrade scikit-learn==1.1.3
!pip install mglearn
import logging
logging.getLogger('matplotlib.font_manager').setLevel(logging.ERROR)
import mglearn
from sklearn.model_selection import train_test_split
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
import seaborn as sns
%matplotlib inline
Linear Regression
- 단순 선형 회귀 분석(Simple Linear Regression Analysis)
- 다중 선형 회귀 분석(Multiple Linear Regression Analysis)
정규화(Regularization)
모델을 학습할 때는 비용(cost) 즉, 오류를 최소화하는 방향으로 진행한다.
- L1 Regularization

- L2 Regularization

Linear Regression
- Linear Regression
from sklearn.linear_model import LinerRegression
# 데이터 로드
X, y = mglearn.datasets.load_extended_boston()
# 데이터 분리
X_tr, X_te, y_tr, y_te = train_test_split(X, y, test_size=0.25, random_state=0)
# 선형 회귀 모델 정의
lr = LinearRegression()
# 모델 학습
lr.fit(X_tr, y_tr)
# bias: lr.intercept_
# weights: lr.coef_
# 모델을 이용한 검증 데이터 예측
pred = lr.predict(X_te)
# 모델 평가
print(f'훈련용 평가지표: {lr.score(X_tr, y_tr)} / 테스트용 평가지표: {lr.score(X_te, y_te)}')
# 훈련용 평가지표: 0.9520519609032728 / 테스트용 평가지표: 0.6074721959665773- Ridge with L2
from sklearn.linear_model import Ridge
ridge = Ridge().fit(X_tr, y_tr)
print(f'훈련용 평가지표: {ridge.score(X_tr, y_tr)} / 테스트용 평가지표: {ridge.score(X_te, y_te)}')
# 훈련용 평가지표: 0.8857966585170941 / 테스트용 평가지표: 0.7527683481744751
# alpha 값을 낮추면 규제의 효과가 없어서 overfitting 가능성이 높아진다.
ridge01 = Ridge(alpha=0.1).fit(X_tr, y_tr)
print(f'훈련용 평가지표: {ridge01.score(X_tr, y_tr)} / 테스트용 평가지표: {ridge01.score(X_te, y_te)}')
# 훈련용 평가지표: 0.9282273685001992 / 테스트용 평가지표: 0.7722067936479814
# alpha 값을 높이면 훈련 세트의 성능은 나빠지지만 일반화에는 도움을 줄 수 있다.
ridge10 = Ridge(alpha=10).fit(X_tr, y_tr)
print(f'훈련용 평가지표: {ridge10.score(X_tr, y_tr)} / 테스트용 평가지표: {ridge10.score(X_te, y_te)}')
# 훈련용 평가지표: 0.7882787115369614 / 테스트용 평가지표: 0.635941148917731
plt.figure(figsize=(10,8))
plt.plot(ridge10.coef_, '^', label='Ridge alpha=10')
plt.plot(ridge.coef_, 's', label='Ridge alpha=1')
plt.plot(ridge01.coef_, 'v', label='Ridge alpha=0.1')
plt.plot(lr.coef_, 'o', label='LinearRegression')
plt.xlabel('alpha list') # 계수 목록
plt.ylabel('alpha size') # 계수 크기
plt.hlines(0, 0, len(lr.coef_))
plt.ylim(-25, 25)
plt.legend()
- Lasso with L1
from sklearn.linear_model import Lasso
lasso = Lasso().fit(X_tr, y_tr)
print(f'훈련용 평가지표: {lasso.score(X_tr, y_tr)} / 테스트용 평가지표: {lasso.score(X_te, y_te)}')
print('-'*80)
print(f'사용한 특성의 수: {np.sum(lasso.coef_ != 0)} / 전체 특성 수: {X_tr.shape[1]}')
# 훈련용 평가지표: 0.29323768991114607 / 테스트용 평가지표: 0.20937503255272294
# --------------------------------------------------------------------------------
# 사용한 특성의 수: 4 / 전체 특성 수: 104
lass001 = Lasso(alpha=0.01, max_iter=100000).fit(X_tr, y_tr)
print(f'훈련용 평가지표: {lass001.score(X_tr, y_tr)} / 테스트용 평가지표: {lass001.score(X_te, y_te)}')
print('-'*80)
print(f'사용한 특성의 수: {np.sum(lass001.coef_ != 0)} / 전체 특성 수: {X_tr.shape[1]}')
# 훈련용 평가지표: 0.9507158754515463 / 테스트용 평가지표: 0.6437467421272821
# --------------------------------------------------------------------------------
# 사용한 특성의 수: 96 / 전체 특성 수: 104
lass00001 = Lasso(alpha=0.0001, max_iter=100000).fit(X_tr, y_tr)
print(f'훈련용 평가지표: {lass00001.score(X_tr, y_tr)} / 테스트용 평가지표: {lass00001.score(X_te, y_te)}')
print('-'*80)
print(f'사용한 특성의 수: {np.sum(lass00001.coef_ != 0)} / 전체 특성 수: {X_tr.shape[1]}')
# 훈련용 평가지표: 0.9507158754515463 / 테스트용 평가지표: 0.6437467421272821
# --------------------------------------------------------------------------------
# 사용한 특성의 수: 96 / 전체 특성 수: 104plt.figure(figsize=(10,8))
plt.plot(lasso.coef_, 's', label='Lasso alpha=1')
plt.plot(lass001.coef_, '^', label='Lasso alpha=0.01')
plt.plot(lass00001.coef_, 'v', label='Lasso alpha=0.0001')
plt.plot(ridge01.coef_, 'o', label='Ridge alpha=0.1')
plt.xlabel('alpha list') # 계수 목록
plt.ylabel('alpha size') # 계수 크기
plt.hlines(0, 0, len(lr.coef_))
plt.ylim(-25, 25)
plt.legend(ncol=2, loc=(0, 1.05))
- ElasticNet
from sklearn.linear_model import ElasticNet
elnet = ElasticNet().fit(X_tr, y_tr)
print(f'훈련용 평가지표: {elnet.score(X_tr, y_tr)} / 테스트용 평가지표: {elnet.score(X_te, y_te)}')
print('-'*80)
print(f'사용한 특성의 수: {np.sum(elnet.coef_ != 0)} / 전체 특성 수: {X_tr.shape[1]}')
# 훈련용 평가지표: 0.32837814485847916 / 테스트용 평가지표: 0.2217004367773664
# --------------------------------------------------------------------------------
# 사용한 특성의 수: 38 / 전체 특성 수: 104
alpha=0.01
ratios = [0.2, 0.5, 0.8]
for ratio in ratios:
elnet = ElasticNet(alpha=alpha, l1_ratio=ratio, random_state=42).fit(X_tr, y_tr)
print(f'ratio: {ratio}')
print(f'훈련용 평가지표: {elnet.score(X_tr, y_tr)} / 테스트용 평가지표: {elnet.score(X_te, y_te)}')
print(f'사용한 특성의 수: {np.sum(elnet.coef_ != 0)} / 전체 특성 수: {X_tr.shape[1]}')
print('-'*80)
# ratio: 0.2
# 훈련용 평가지표: 0.8421033820826037 / 테스트용 평가지표: 0.7055067157435387
# 사용한 특성의 수: 93 / 전체 특성 수: 104
# --------------------------------------------------------------------------------
# ratio: 0.5
# 훈련용 평가지표: 0.8553665697077995 / 테스트용 평가지표: 0.7209054027265394
# 사용한 특성의 수: 84 / 전체 특성 수: 104
# --------------------------------------------------------------------------------
# ratio: 0.8
# 훈련용 평가지표: 0.8752442706471416 / 테스트용 평가지표: 0.741439523522267
# 사용한 특성의 수: 63 / 전체 특성 수: 104
# --------------------------------------------------------------------------------
alphas=[0.001, 0.01, 0.1]
ratio = 0.8
for alpha in alphas:
elnet = ElasticNet(alpha=alpha, l1_ratio=ratio, random_state=42).fit(X_tr, y_tr)
print(f'alpha: {alpha}')
print(f'훈련용 평가지표: {elnet.score(X_tr, y_tr)} / 테스트용 평가지표: {elnet.score(X_te, y_te)}')
print(f'사용한 특성의 수: {np.sum(elnet.coef_ != 0)} / 전체 특성 수: {X_tr.shape[1]}')
print('-'*80)
# alpha: 0.001
# 훈련용 평가지표: 0.9271504286329 / 테스트용 평가지표: 0.7813331506633265
# 사용한 특성의 수: 91 / 전체 특성 수: 104
# --------------------------------------------------------------------------------
# alpha: 0.01
# 훈련용 평가지표: 0.8752442706471416 / 테스트용 평가지표: 0.741439523522267
# 사용한 특성의 수: 63 / 전체 특성 수: 104
# --------------------------------------------------------------------------------
# alpha: 0.1
# 훈련용 평가지표: 0.7399596108844948 / 테스트용 평가지표: 0.5768205411208096
# 사용한 특성의 수: 33 / 전체 특성 수: 104
# --------------------------------------------------------------------------------
2. Supervised Learning - Classification
2-1. Confusion Matrix
혼동행렬(Confusion Matrix)
- 예측과 실제 값 사이의 관계를 행렬로 표현한 것을 말한다.

- Sensitivity(Recall): 민감도(재현도)
- 실제로 참인 것들 중에 예측이 참인 비율
- Specificity: 특이도
- Precision: 정밀도
- 예측이 참인 것들 중에 실제로 참인 비율
- Accuracy: 정확도
- 전체 문제 중에서 정답을 맞힌 비율
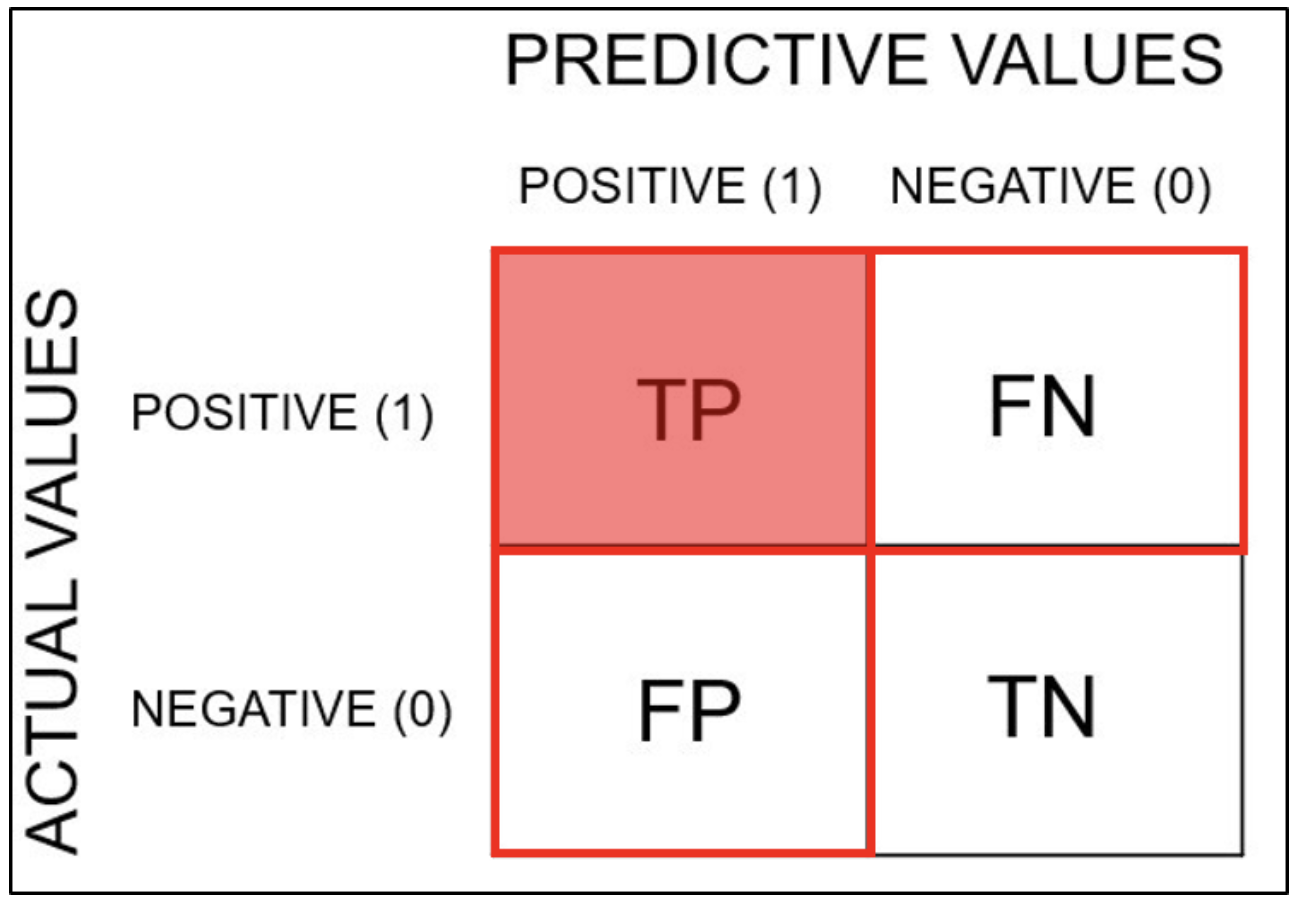
- TP(True Positive, 참긍정)
- 예측이 참인데 실제로도 참인 경우
- TN(True Negative, 참부정)
- 예측이 거짓인데 실제로도 거짓인 경우
- FP(False Positive, 거짓긍정)
- 예측이 참인데 실제로는 거짓인 경우
- FN(False Negative, 거짓부정)
- 예측이 거짓인데 실제로는 참인 경우
코드 구현
- Load Data
import numpy as np
import pandas as pd
from sklearn.datasets import load_digits
digits = load_digits()
digits.data[0].reshape(8, 8)import matplotlib.pyplot as plt
plt.imshow(digits.data[0].reshape(8, 8))
plt.colorbar()
plt.show()
data = digits.data
# Binary Classifier(이진 분류)
target = (digits.target == 5).astype(int)from sklearn.model_selection import train_test_split
SEED = 42
x_train, x_valid, y_train, y_valid = train_test_split(data, target, random_state=SEED)
digit = data[5]import matplotlib as mpl
import matplotlib.pyplot as plt
import seaborn as sns
digit_img = digit.reshape(8, 8)
plt.imshow(digit_img, cmap="gray")
plt.axis("off")
plt.show()
- Modeling
from sklearn.linear_model import SGDClassifier
sgd_clf = SGDClassifier(random_state=42)
sgd_clf.fit(x_train, y_train)
sgd_clf.predict([digit])from sklearn.model_selection import cross_val_predict
y_train_pred = cross_val_predict(sgd_clf, x_train, y_train, cv=10)- Confusion Matrix
from sklearn.metrics import confusion_matrix
conf_mx = confusion_matrix(y_train, y_train_pred, normalize="true")
plt.figure(figsize=(7,5))
sns.heatmap(conf_mx, annot=True, cmap="coolwarm", linewidth=0.5)
plt.xlabel('Predicted')
plt.ylabel('Actual')
plt.show()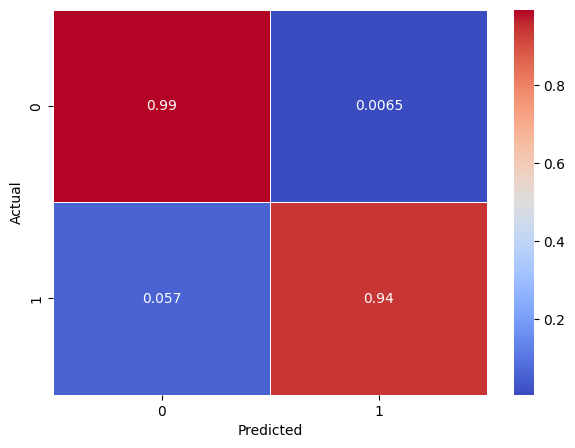
평가지표
- Dummy 예측
from sklearn.dummy import DummyClassifier
# 모델 정의
dummy = DummyClassifier(strategy='most_frequent')
# 모델 학습
dummy.fit(x_train,y_train)
# 모델 예측
pred_dummy = dummy.predict(x_valid)- 모델 예측
from sklearn.linear_model import SGDClassifier
# 모델 정의
sgd_clf = SGDClassifier(random_state=42)
# 모델 학습
sgd_clf.fit(x_train, y_train)
# 모델 예측
pred_clf = sgd_clf.predict(x_valid)- Accuracy(정확도)
- 음성(0)이 양성(1)보다 훨씬 많은 경우, 음성(0)으로만 예측해도 높은 정확도를 보이기 때문에 적절한 성능지표가 될 수 없다.


from sklearn.metrics import accuracy_score
score = accuracy_score(y_valid, pred_dummy)
print(f"dummy: {score}")
score = accuracy_score(y_valid, pred_clf)
print(f"model: {score}")
# dummy: 0.8688888888888889
# model: 0.9866666666666667- Precision(정밀도)
- FP를 줄이는 것이 목표일 때 사용한다.


from sklearn.metrics import precision_score
score = precision_score(y_valid, pred_dummy)
print(f"dummy: {score}")
score = precision_score(y_valid, pred_clf)
print(f"model: {score}")
# dummy: 0.0
# model: 1.0- Sensitivity(민감도) = Recall(재현도)
- FN을 줄이는 것이 목표일 때 사용한다.


from sklearn.metrics import recall_score
score = recall_score(y_valid, pred_dummy)
print(f"dummy: {score}")
score = recall_score(y_valid, pred_clf)
print(f"model: {score}")
# dummy: 0.0
# model: 0.8983050847457628- F1 Score
- 불균형한 데이터가 잘 동작하는지에 대한 평가지표

from sklearn.metrics import f1_score
score = f1_score(y_valid, pred_dummy)
print(f"dummy: {score}")
score = f1_score(y_valid, pred_clf)
print(f"model: {score}")
# dummy: 0.0
# model: 0.9464285714285714from sklearn.metrics import classification_report
print(classification_report(y_valid, pred_dummy))
print('-'*100)
print(classification_report(y_valid, pred_clf))
# precision recall f1-score support
#
# 0 0.87 1.00 0.93 391
# 1 0.00 0.00 0.00 59
#
# accuracy 0.87 450
# macro avg 0.43 0.50 0.46 450
# weighted avg 0.75 0.87 0.81 450
#
# ----------------------------------------------------------------------------------------------------
# precision recall f1-score support
#
# 0 0.98 1.00 0.99 391
# 1 1.00 0.90 0.95 59
#
# accuracy 0.99 450
# macro avg 0.99 0.95 0.97 450
# weighted avg 0.99 0.99 0.99 450- Thresholds(임계값)
pred_proba = sgd_clf.decision_function(x_valid)
threshold = 0 # default
pred = np.where(pred_proba > threshold, 1, 0)
precision_score(y_valid, pred), recall_score(y_valid, pred)
# (1.0, 0.8983050847457628)
threshold = 30000
pred = np.where(pred_proba > threshold, 1, 0)
precision_score(y_valid, pred), recall_score(y_valid, pred)
# (0.0, 0.0)
threshold = -30000
pred = np.where(pred_proba > threshold, 1, 0)
precision_score(y_valid, pred), recall_score(y_valid, pred)
# (0.13111111111111112, 1.0)from sklearn.tree import DecisionTreeClassifier
# 모델 생성
tree = DecisionTreeClassifier(max_depth=3, random_state=SEED)
# 모델 학습
tree.fit(x_train,y_train)
# 모델 평가
pred_tree = tree.predict(x_valid)
tree.predict_proba(x_valid)[0]
# array([0.97628458, 0.02371542]) -> array([0일 확률, 1일 확률])
pred_proba = tree.predict_proba(x_valid)[:, 1]
threshold = 0.5
pred = np.where(pred_proba > threshold, 1, 0)
precision_score(y_valid, pred), recall_score(y_valid, pred)
# (0.9811320754716981, 0.8813559322033898)
threshold = 0.9
pred = np.where(pred_proba > threshold, 1, 0)
precision_score(y_valid, pred), recall_score(y_valid, pred)
# (0.9811320754716981, 0.8813559322033898)
threshold = 0.1
pred = np.where(pred_proba > threshold, 1, 0)
precision_score(y_valid, pred), recall_score(y_valid, pred)
# (0.8813559322033898, 0.8813559322033898)
2-2. Binary Classification
이진 분류 모형
- ROC(Receiver Operating Characteristic) Curve
- FPR를 x축으로, TPR을 y축으로 정의하여 둘 간의 관계를 표현한 그래프


- AUROC(Area Under ROC Curve)
- ROC Curve의 밑부분 면적
- 넓을수록 모형 성능이 좋다.
- 임계값(threshold)과 무관하게 모델의 예측 품질을 측정할 수 있다.
- Poor model: 0.5 ~ 0.7
- Fair model: 0.7 ~ 0.8
- Good model: 0.8 ~ 0.9
- Excellent model: 0.9 ~ 1.0

코드 구현
- Load Data
import numpy as np
import pandas as pd
from sklearn.datasets import load_digits
digits = load_digits()import matplotlib.pyplot as plt
plt.imshow(digits.data[0].reshape(8, 8))
plt.colorbar()
plt.show()
data = digits.data
# Binary Classifier
target = (digits.target == 5).astype(int)from sklearn.model_selection import train_test_split
SEED = 42
x_train, x_valid, y_train, y_valid = train_test_split(data, target, random_state=SEED)- Modeling
from sklearn.dummy import DummyClassifier
dummy = DummyClassifier(strategy='most_frequent')
dummy.fit(x_train,y_train)
pred_dummy = dummy.predict_proba(x_valid)[:,1]from sklearn.tree import DecisionTreeClassifier
tree = DecisionTreeClassifier(max_depth=3, random_state=SEED)
tree.fit(x_train,y_train)
# pred_tree = tree.predict(x_valid)
pred_tree = tree.predict_proba(x_valid)[:,1]- 평가
from sklearn.metrics import roc_curve, auc
fpr, tpr, thresholds = roc_curve(y_valid,pred_dummy)
print(f'dummy: {auc(fpr, tpr)}')
print('-'*50)
fpr, tpr, thresholds = roc_curve(y_valid,pred_tree)
print(f'model: {auc(fpr, tpr)}')
# dummy: 0.5
# --------------------------------------------------
# model: 0.9479604664268065from sklearn.metrics import RocCurveDisplay
fig,ax = plt.subplots()
RocCurveDisplay.from_predictions(y_valid,pred_dummy,ax=ax)
RocCurveDisplay.from_predictions(y_valid,pred_tree,ax=ax)
plt.show()
import seaborn as sns
from sklearn.metrics import confusion_matrix
pred_tree = tree.predict(x_valid)
conf_mx = confusion_matrix(y_valid, pred_tree, normalize="true")
plt.figure(figsize=(7,5))
sns.heatmap(conf_mx, annot=True, cmap="coolwarm", linewidth=0.5)
plt.xlabel('Predicted')
plt.ylabel('Actual')
plt.show()
'SK네트웍스 Family AI캠프 10기 > Daily 회고' 카테고리의 다른 글
| 23일차. Unsupervised Learning (0) | 2025.02.12 |
|---|---|
| 22일차. Supervised Learning - Classification & Ensemble & HPO (0) | 2025.02.11 |
| 20일차. Feature Extraction & Data Encoding (0) | 2025.02.07 |
| 19일차. Machine Learning & Data Preprocessing (0) | 2025.02.07 |
| 18일차. Data Visualization(Seaborn) & Data Cleaning (0) | 2025.02.05 |



